动态图学习 Dynamic Graph Learning
动态图的表示方法
动态图的直观表现就是,图中的节点数量、边的数量、节点特征、边的连接关系类型、边权重等都可能随时间变化而改变。有两种方式可以表示动态图,离散型和连续型。
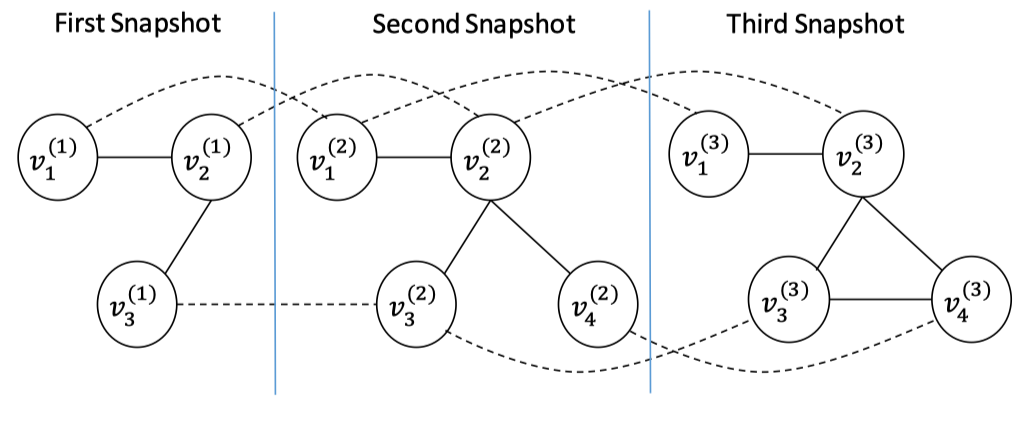
离散型(Discrete-Time Dynamic Graph,DTDG) 一般用图快照序列来表示。每个快照是一个静态图,典型的是时空图,例如交通流预测。
连续型(Continuous-Time Dynamic Graph,CTDG) 由一个初始的静态图以及一系列事件来表示。
一般情况离散型是连续型的特例。
动态图学习
这里主要介绍的是离散型的图学习,更适用于交通流预测场景。
隐式建模时间特征
这一类方法对时间这一维度进行隐式的建模,对外表现为把动态图转换为静态图。
时间性聚合:对于仅仅是图结构(邻接矩阵)变化的情况,将不同快照的邻接矩阵进行加权聚合;如果节点特征也变化,则也可以对特征进行加权聚合。
\[\boldsymbol{A}^{(a g g)}=\sum_{t=1}^\tau \phi(t, \tau) \boldsymbol{A}^{(t)}\]对于连续型动态图的表示,可以转化为离散型,再使用上述方法。
时间解卷:连接在不同的时间的同一个节点。将相邻的时间点的节点连接,变成一个更大的静态图。
显式建模时间特征
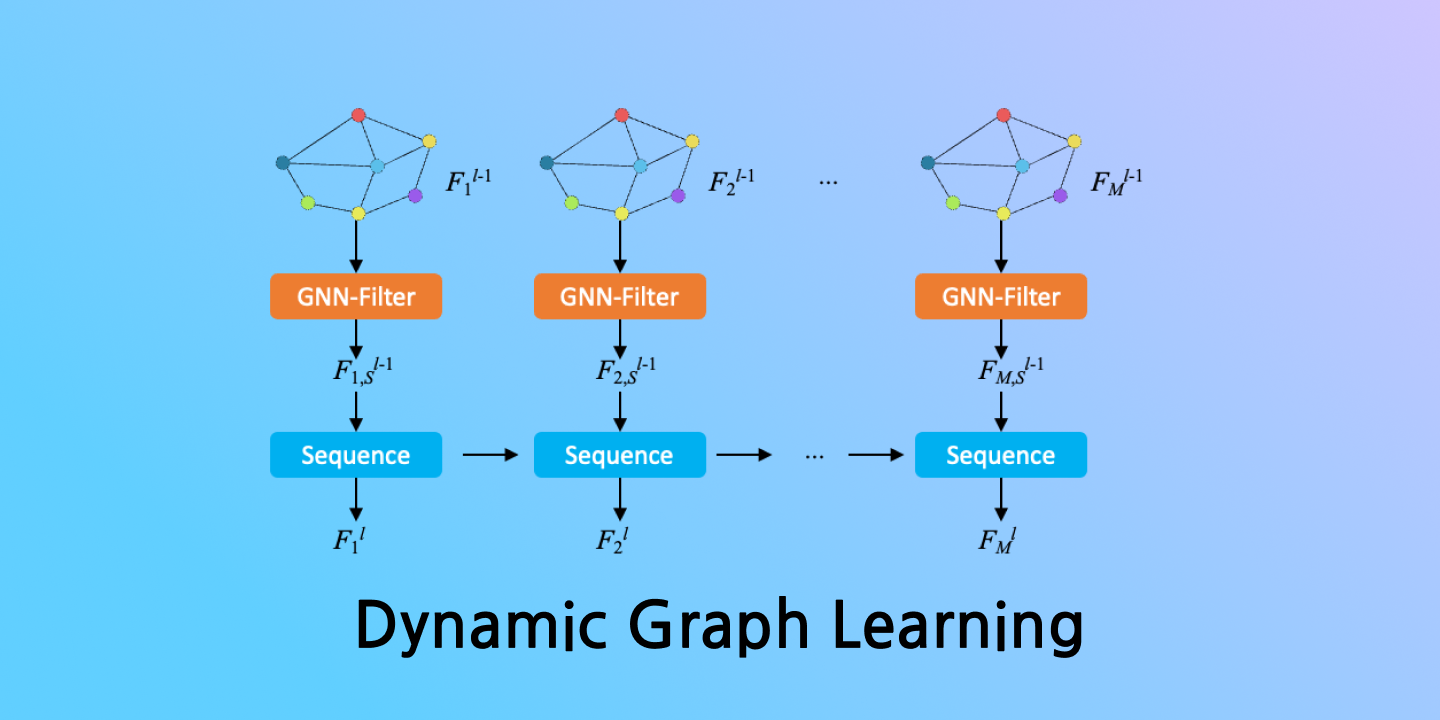
GNN-RNN:对每个快照进行GCN图卷积,然后得到的序列输入进RNN模型。这一个里每个节点都是同一个RNN模型。
\[\begin{aligned}& \boldsymbol{Z}^{(t)}=\operatorname{GCN}\left(\boldsymbol{X}^{(t)}, \boldsymbol{A}^{(t)}\right) \\& \boldsymbol{H}^{(t)}, \boldsymbol{C}^{(t)}=\operatorname{LSTM}\left(\boldsymbol{Z}^{(t)}, \boldsymbol{H}^{(t-1)}, \boldsymbol{C}^{(t-1)}\right)\end{aligned}\]RNN-GNN:对于邻接矩阵不变的情况也可以先时序模型,再GNN模型。
\[\begin{aligned}& \boldsymbol{H}^{(t)}, \boldsymbol{C}^{(t)}=L S T M\left(\boldsymbol{X}^{(t)}, \boldsymbol{H}^{(t-1)}, \boldsymbol{C}^{(t-1)}\right) \\& \boldsymbol{Z}^{(t)}=G C N\left(\boldsymbol{H}^{(t)}, \boldsymbol{A}\right)\end{aligned}\]这仅适合于邻接矩阵不变的情况,否则该模型无法捕捉到图结构的变化。上面GNN-RNN能捕捉到是因为每个快照都GCN聚合了,每个快照中节点能反映本快照内的结构信息,所以再送入RNN模型就可以捕捉到结构的变化了。
GNN-Transformer:类似GNN-RNN方法。对节点特征运用GCN后,再加上位置编码信息。
\[\begin{aligned}& \boldsymbol{Z}^{(t)}=\operatorname{GCN}\left(\boldsymbol{X}^{(t)}, \boldsymbol{A}^{(t)}\right) \text { for } t \in\{1,2, \ldots, \tau\} \\& \boldsymbol{H}_t^{(0, i)}=\boldsymbol{Z}_i^{(t)}+\boldsymbol{p}^{(t)} \text { for } t \in\{1,2, \ldots, \tau\}, i \in\{1,2, \ldots,|V|\} \\& \boldsymbol{H}^{(L, i)}=\text { Transformer }\left(\boldsymbol{H}^{(0, i)}, \tilde{\boldsymbol{A}}\right) \text { for } i \in\{1,2, \ldots,|V|\}\end{aligned}\]- GNN-CNN:与上述方法类似,一般用一维卷积模型。
- 创建更深的模型:例如GNN-RNN,可以堆叠多个模块,组合挖掘深层信息。
CTDG 学习
这里对该类表示的动态图学习进行简要介绍。这一类模型的恶思想是按顺序消耗观测值,对某个节点进行新的观测时更新该节点的嵌入。
应用
对于城市交通控制,交通预测起着至关重要的作用。要预测一条道路的未来交通,需要考虑两个重要因素:空间依赖性和时间依赖性。不同道路的交通量在空间上是相互依赖的,因为一条道路的未来交通量取决于与其相连的道路的交通量。空间依赖性是道路网络拓扑结构的一个功能。每条道路也有时间上的依赖性,因为一条道路在任何时候的交通量都取决于以前的交通量。还存在周期性模式,例如,一条道路的交通量在一天中的相同时间或一周中的相同时间可能是相似的。